数据结构之链表

I. 链表

线性表由储存结构可以分为顺序表 sequence list 和链表 linked list。 顺序表由于插入和删除时需要移动大量的元素，所以非常耗费时间，所以就引出了链表

1. 什么是链表

链表 linkedlist

  • 一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的
  • 存储的数据元素可以存在内存中未被占用的任意位置
  • 对每个数据元素 ai 的存储映像来说，我们称之为结点 Node, 每个结点包括两个部分
    • 数据域：存储数据元素信息
    • 指针域：存储指向当前结点直接后继的存储位置

II.单链表

1.什么是单链表

单链表：

  • n 个结点连接成一个链表，即线性表 （a0, a1...an) 的链式存储结构
  • 此链表的每个结点，只包含一个指针域
  • 最后一个结点的指针为空 null，因为没有后继结点
  • 头结点：
    • 在单链表的第一个结点前设置一个结点
    • 头结点不存储任何信息，只存储头指针
    • 头指针 ： 第一个结点的存储位置
  • 可以把单链表想象成火车，每一个结点是一个车厢，火车头就是头结点

单链表图示如下：

单链表

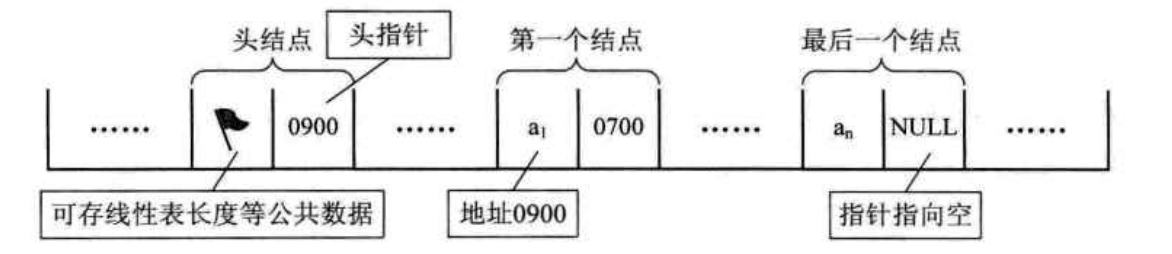
注意， 头指针和头结点的区别：

  • 头指针
    • 是链表指向第一个结点的指针，若链表有头结点，那么则是指向头结点的指针
    • 头指针有标识作用，通常用头指针冠以链表的名字
    • 无论链表是否为空，头指针都不会是空
    • 头指针是链表的必要元素
  • 头结点
    • 头结点是为了操作的统一和方便而设立的，放在第一元素的结点之前
    • 其数据域一般无意义，也可以存放链表的长度
    • 有个头结点，对第一个元素结点的操作就和其他结点相统一了
    • 头结点不是链表的必要元素

2. 单链表的实现

代码请参见DataStructure-Java/src/org/lovian/datastructure/linearlist/linkedlist/SingleLinkedList.java

在内存中每个结点并不是连续存放的，链表只是表示线性表中的数据元素及数据元素之间的逻辑关系。

单链表的存储示意图如下：

单链表2

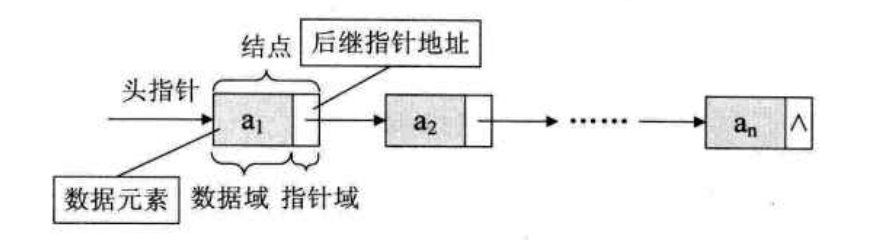
如果带有头结点：

单链表3

空链表如下

单链表4

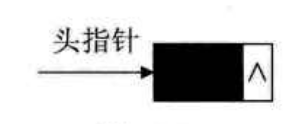
A. 单链表的数据结构定义

我们用java来实现，一个链表结点，包括了数据域和指针域构成，我们设定一个链表一定有一个头结点，头结点包含一个头指针

package org.lovian.datastructure.linearlist.linkedlist;

import org.lovian.datastructure.linearlist.datatype.DataType;

/**
 * 单链表的实现
 * @author Zhengshuai PENG
 *
 */
public class SingleLinkedList {

	// 头结点
	private Node linkedList;

	public SingleLinkedList() {
		super();
		this.linkedList = new Node();
	}



}

/**
 * 单链表结点
 *
 */
class Node {
	// 数据域
	private DataType data;
	// 指针域
	private Node next;

	public DataType getData() {
		return data;
	}

	public void setData(DataType data) {
		this.data = data;
	}

	public Node getNext() {
		return next;
	}

	public void setNext(Node next) {
		this.next = next;
	}
}

B. 单链表的读取

单链表中第 i 个元素的位置（这里 i 是索引，从 0 开始计）在哪，我们没法直接直到，所以必须要从头开始找

获取链表第 i 个位置的数据算法思路如下：

  • 拿到链表的第一个结点 p， 初始化 j 从 0 开始
  • 如果 j < i, 就遍历链表，让 p 的指针向后移动，不断指向下一个结点， j 累计加 1
  • 如果链表的末尾 p 为空，则说明第 i 个元素不存在
  • 否则查找成功，返回结点 p 的数据
public boolean getElem(int i, DataType element) {

	int j = 0;

	if (i < j)
		return false;

	// 拿到链表的第一个结点
	Node p = linkedList.getNext();

	// p 如果不为空，或者计数器不等于 i 时
	// 当 i = j 时，跳出循环，
	while (p != null && j < i) {
		// 让 p 指向下一个结点
		p = p.getNext();
		++j;
	}

	// 跳出循环后，如果p为空，说明不存在
	if (p == null)
		return false;

	// 取出目标元素的值
	element.SetData(p.getData().getData());
	return true;
}

注意：

  • 算法简单来说，就是从头开始找，直到第 i 个元素为止，算法复杂度取决于 i 的位置，最坏的情况为 O(n)
  • 由于单链表结构没有定义表长，所以不能事先知道要循环多少次，所以不方便用for来控制循环，其核心思想是工作指针后移

C. 单链表的插入

单链表插入很简单，

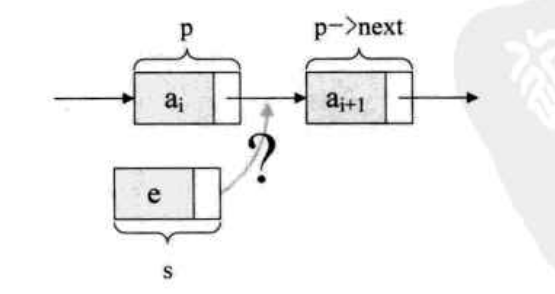
单链表插入

如果要在 p 和 p->next 之间插入结点 s， 只需要让改变 p 的指针域 和 s 的指针域：

s->next = p->next;
p->next = s;

也就是说，让原来 p 结点的后继结点变成 s 的后继结点，在把 s 称为 p 结点的后继结点，注意这两个顺序不能反，所以要先找到目标位置的前驱结点，即 p

插入算法思路：

  • 拿到链表的头结点 p，初始化 j 从 0 开始
  • 当 j < i 时，就遍历链表，让 p 的指针向后移动，不断指向下一个结点，j累计加1
  • 若到链表末尾时 p 为空，则说明第 i 个元素不存在
  • 否则查找成功，在系统中生成一个空结点 s
  • 将数据元素 e 赋值给 s-> data
  • 单链表插入标准语句 s->next = p->next; p->next = s;
  • 返回成功

java代码实现如下

public boolean listInsert(int i, DataType element) {
	int j = 0;
	if (i < j)
		return false;

	// 获取头结点
	Node p = linkedList;
	// // 找到目标位置的前驱结点
	while (p != null && j < i) {
		p = p.getNext();
		++j;
	}

	if (p == null)
		return false;

	// 新建结点
	Node s = new Node();
	s.setData(element);
	// 插入到前驱结点之后
	s.setNext(p.getNext());
	p.setNext(s);

	return true;
}

D.单链表的删除

单链表的删除：

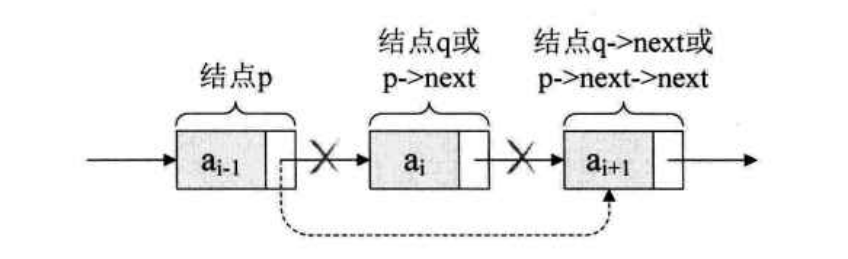
单链表删除

如果要删除结点 q， 那么就是将它的前驱结点的指针指向它的后继结点：

q = p->next;
p->next = q->next; // p->next = p->next->next;

所以也是要找到要删除元素的前驱结点

删除操作的算法思路：

  • 拿到链表的头结点 p， 初始化 j 从 0 开始
  • 当 j < i 时，就遍历链表，让 p 的指针向后移动，不断指向下一个结点，j累计加1
  • 若到链表末尾时 p 为空，则说明第 i 个元素不存在
  • 否则查找成功，把待删除结点 p->next 赋值给 q
  • 单链表删除语句 p->next = q->next
  • 将 q 结点中的数据赋值给 e，作为返回
  • 释放 q 结点（C/C++）
  • 返回成功

java代码实现如下

public boolean listDelete(int i, DataType element) {
	int j = 0;
	if (i < j)
		return false;

	Node p = linkedList;

	// 找到目标位置的前驱结点
	while (p.getNext() != null && j < i) {
		p = p.getNext();
		++j;
	}

	if (p.getNext() == null)
		return false;
	// 将目标元素命名为 q，即待删除元素
	Node q = p.getNext();
	// 单链表删除
	// p->next = q.next
	// p->next = p->next->next;
	p.setNext(q.getNext());
	// 返回被删除的元素的值返回
	element.SetData(q.getData().getData());
	return true;
}

插入和删除操作都是由两部分组成：

  • 第一部分遍历查找 i 个元素
  • 第二部分就是插入和删除操作

插入和删除算法复杂度： O(n)，如果我们不知道第 i 个元素的位置，在插入一个数据的时候，链表和顺序表的时间复杂度相同，但是，如果要从第 i 个位置插入10个元素，对顺序表来说，每次插入就需要移动 n-i 个元素，每次都是 O（n）; 而单链表则是第一次找到 i 个位置，此时为 O（n），接下来其他元素的插入只是通过赋值来移动指针，时间复杂度是 O（1），所以对于插入或者删除数据越频繁的操作，单链表的效率优势就越明显

E. 链表清空操作

算法思路如下：

  • 拿到链表的头结点 p， 声明一个结点q
  • 循环
    • 将 p 的下一个结点赋值给 q
    • 释放 p
    • 将 q 赋值给 p

java代码实现如下

public void clear() {
	Node p = linkedList;
	Node q = null;
	while (p != null) {
		q = p.getNext();
		p.setData(null);
		p.setNext(null);
		p = q;
	}
}

F. 链表的反转

反转链表有两种思路：

  • 建立新链表
    • 遍历旧的链表，每拿到一个结点，就把它插入到新链表的开头
  • 直接修改链表结点的指针域
    • 遍历链表，每拿到一个结点，把它的指针域设置成它的前驱结点
    • 最后把头结点指向原来的最后一个结点

这里用的是第二种思路来实现：

public void reverseList() {

	// 获取原链表的第一个元素
	Node head = linkedList.getNext();
	// 如果链表为空或者只有一个元素，不需要反转
	if (head == null || head.getNext() == null)
		return;

	// 定义第一个元素为新的最后一个结点
	Node newLast = head;
	// 前一个结点
	Node previous = head;
	// 当前结点
	Node current = head.getNext();

	// 循环到最后一个结点之前
	while (current.getNext() != null) {
		// 下一个结点
		Node next = current.getNext();
		// 把当前结点的下一个结点设置成前一个结点
		current.setNext(previous);
		// 移动结点指针
		previous = current;
		current = next;
	}
	// 找到最后一个元素结点，把它定义成新链表的第一个元素结点
	Node newHead = current;
	newHead.setNext(previous);
	// 将头结点指向新的第一个元素结点
	linkedList.setNext(newHead);
	// 新的最后一个结点末尾指针设置为空
	newLast.setNext(null);
}

3. 单链表结构和顺序表的对比

存储分配方式

  • 顺序表：用一段连续的存储单元依次存储线性表的数据元素
  • 单链表： 采用链式存储结构，用一组任意的存储单元存放线性表的元素

时间性能

  • 查找：
    • 顺序表： O(1)
    • 单链表： O(n)
  • 插入和删除：
    • 顺序表： 需要平均移动表长一半的元素，时间为 O(n)
    • 单链表： 在找到某个位置的指针之后，插入和删除的时间仅为 O(1)

空间性能

  • 顺序表：需要预分配存储空间，大了浪费，小了则容易溢出
  • 单链表：不需要分配存储空间，只要有就可以分配，元素个数不受限制

III. 其他链表

1.静态链表

在没有指针的语言中，我们上面的单链表是没法实现的，所以，就用数组来代替指针。

数组中的每个元素都是由两个数据域组成：（二维数组）

  • data ： 存放数据元素
  • cursor ： 存放当前元素后继结点的数组下标，相当于 next 指针

这种链表就叫做静态链表， 它的实现方法称之为游标实现法。

  • 静态链表优点：
    • 插入和删除操作只需要修改游标，不需要移动元素，从而改进了顺序表中插入和删除需要移动大量元素的缺点
  • 静态链表缺点：
    • 没有解决连续存储带来的表长难以确定的问题，失去了顺序结构随机存取的特性

2. 循环链表

循环链表， circular linked list: 将单链表尾结点的指针指向头结点，就使得单链表形成了一个环，这种头尾相接的单链表称为单循环链表

循环链表

一个空的循环列表则如下

循环链表1

循环链表的尾指针

在单链表中，有了头结点，我们可以用 O(1) 的时间访问第一个结点，但对于要访问的最后一个结点，则需要 O(n) 的时间，我们要扫描整个链表。所以循环链表中把头指针变成尾指针 rear，用来指向尾结点的指针：

尾指针

有了这个尾指针，查找尾结点是 O(1), 查找开始结点，就是 rear->next->next, 复杂度也是 O(1)

循环链表的操作

循环链表的操作和单链表一样，唯一的区别就是在循环的条件里，单链表是判断 p->next 是否为空，而在循环链表里，则是判断 p->next 是否是头结点

3. 双向链表

由于单向链表有 next 指针，所以查找下一个结点复杂度是 O（1），但是查找上一个结点可能就需要 O(n) 的复杂度了，那么为了克服这个缺点，就引出了双向链表 double linked list。

双向链表有三个域，一个数据域和两个指针域：

  • 数据域 ：存放数据元素
  • 前驱指针域 ：存放前驱结点的指针
  • 后继指针域 ：存放后继结点的指针

双向链表也可以是循环链表，当然由于是循环的，所以只需要头指针，图示如下：

双向链表

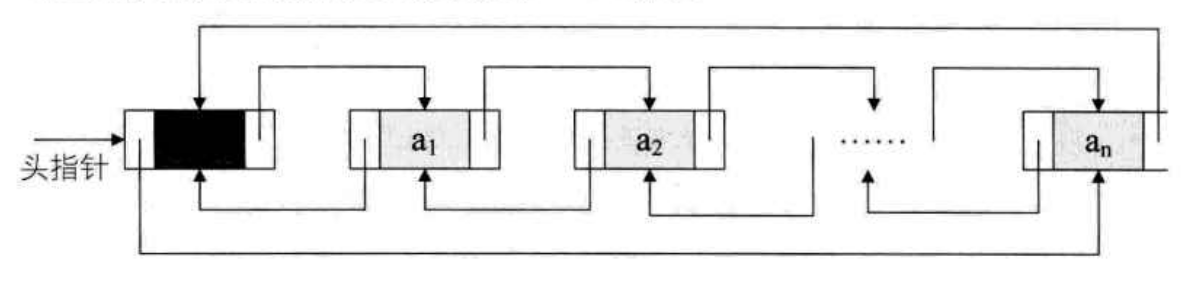
空的双向循环列表则如下：

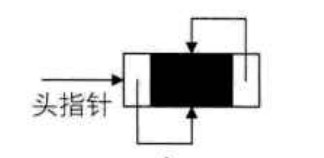
空双向链表

双向链表的代码实现请参考 https://github.com/ZhengshuaiPENG/DataStructure-Java/tree/master/src/org/lovian/datastructure/linearlist/doublelinkedlist

双向链表的操作

双向链表的基本操作和单链表相同，有区别的就是插入操作，删除操作和反转操作

A. 插入操作

假设我们有一个存储着数据元素 e 的结点 s，要把它插入到结点 p 之后， 结点 p->next 之前，那么需要下面几步：

s -> prior = p;				// 设置 p 结点为 s 结点的前驱结点
s -> next = p -> next;		// 设置 p->next 结点为 s结点的后继结点
p -> next -> prior = s;     // 原先 p 结点的后继结点的前驱设置成 s
p -> next = s; 				// p结点的后继设置成 s

就是说， 先搞定待插入结点 s 的前驱和后继，然后搞定原来后继结点的前驱，最后解决前结点的后继

B. 删除操作

删除比插入简单，比如我们要删除结点 p， 那么 p 的前驱是 p->prior, p的后继是 p->next, 那么只需要做下面两步：

p->prior->next = p->next;		// 把 p->next 设置成 p->prior 的后继
p->next->prior = p->prior;		// 把 p->prior 设置成 p->next 的前驱

双向链表的优点

具有良好的对称性，对某个结点的前后结点的操作，比单链表效率更高，但是占用了略多一点的空间，所以就是以空间来换时间

Share this on