数值结构之队列 Queue

I. 队列

1. 栈与队列

  • 栈 Stack ： 是限定仅在表尾为进行插入和删除操作的线性表
  • 队列 Queue ：是只允许在一段进行插入操作，而在另一端进行删除操作的线性表

2. 什么是队列

队列 Queue：

  • 只允许在一端进行插入操作，另一端进行删除操作的线性表
  • 允许插入的一端称之为队尾
  • 允许删除的一端称之为队头
  • 队列是一种先进先出 FIFO 的线性表
    • FIFO： First In First Out
  • 举例：排队

队列的示意图：

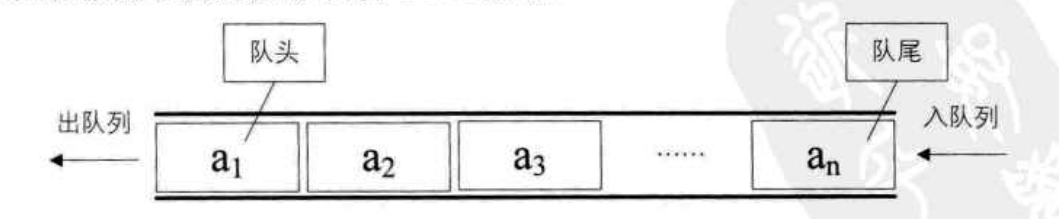
Queue

II. 队列的实现

1. 队列的抽象数据类型

队列的底层也是线性表，所以队也也有类似线性表的各种操作，不同的就是插入数据只能在队尾进行，删除数据只能在队头进行

ADT Queue
Data
	DataType {a0, a2, ..., an−1}
Operation
	InitQueue(*Q)			// 初始化操作，建立一个空队列 Q
	DestroyQueue(*Q)		// 若队列 Q 存在，则销毁它
	ClearQueue(*Q)			// 将队列 Q 清空
	QueueEmpty(Q)			// 若队列 Q 为空，返回 true，否则返回 false
	GetHead(Q, *e)			// 若队列存在且非空，用 e 返回队列 Q 的队头元素
	EnQueue(*Q, e)			// 若队列 Q 存在，插入新元素 e 到队列 Q 中并成为队尾元素
	DeQueue(*Q, *e)			// 删除队列 Q 中队头元素，并用 e 返回其值
	QueueLength(Q)			// 返回队列 Q 的元素个数
endADT

2. 队列的顺序存储结构

既然队列是一种线性表，所以也有顺序存储结构，即底层是数组的结构。

但是顺序存储结构存在不足： 假设有一个队列有 n 个元素，则顺序存储的队列需要建立一个大于 n 的数组，并把队列的所以元素存储在数组的前 n 个单元，数组下标为 0 的一段即是队头。而入队列操作其实就是就在队尾添加一个元素，不需要移动其他元素，因此时间复杂度为 O(1); 但是，队列元素的出列元素是队头，即下标为 0 的位置，那么，当队列中的元素出列，后面所有的元素都得跟着向前移动，以保证队列的队头，也就是下标为 0 的位置不为空，所以时间复杂度为 O(n)。

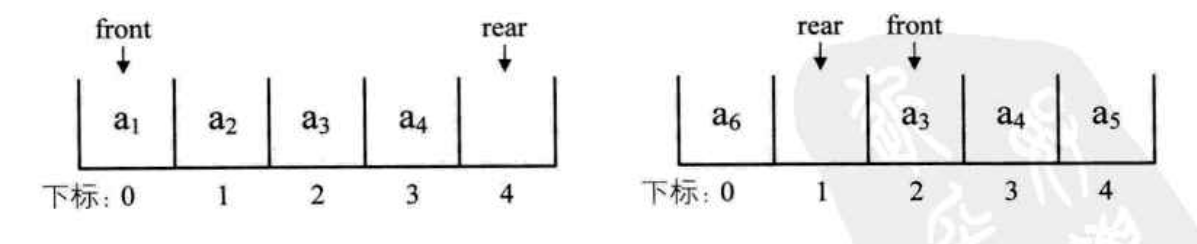
队列的顺序存储结构实现和顺序表完全相同，下图是顺序队列的入列图示：

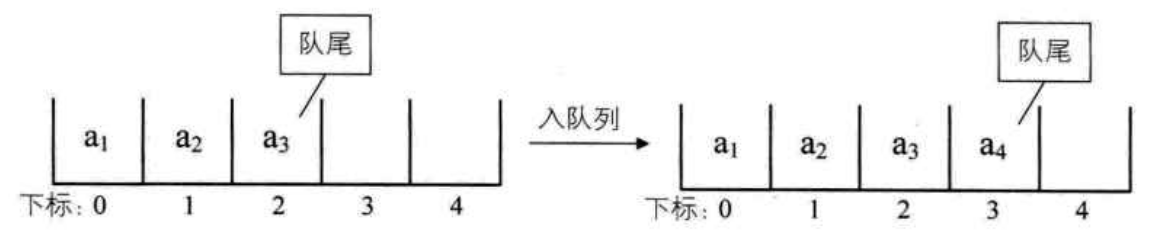
enQueue

而下图，则是队列出列操作：

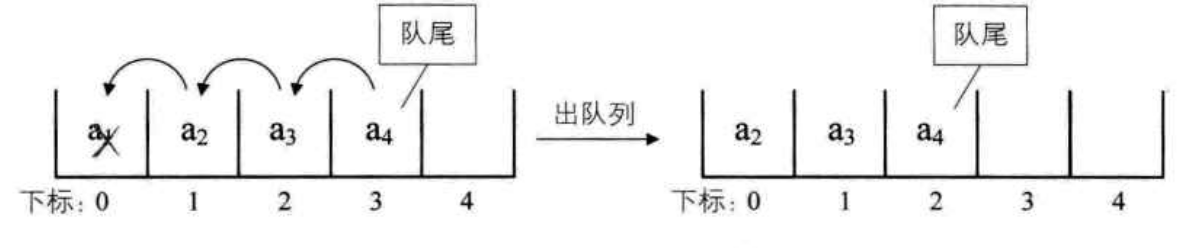
deQueue

3. 循环队列

为了解决顺序存储队列的出列的时间复杂度问题，我们增加了两个指针：

  • 队头指针： front ，指向队列的队头元素
  • 队尾指针： rear， 指向队尾元素的下一个位置
  • 当 front 等于 rear 时，代表空对列

图示如下

QueuePointer

引入了 front 指针和 rear 指针后， 队列的出列操作就可以不用移动元素了，只需要移动指针就会可以了。但是，由于 rear 指针指向的是队尾元素的下一个位置，如果队尾元素刚好在数组的最后一个位置上，那么，rear 指针就指向数组之外了，这样就溢出了。

图示如下

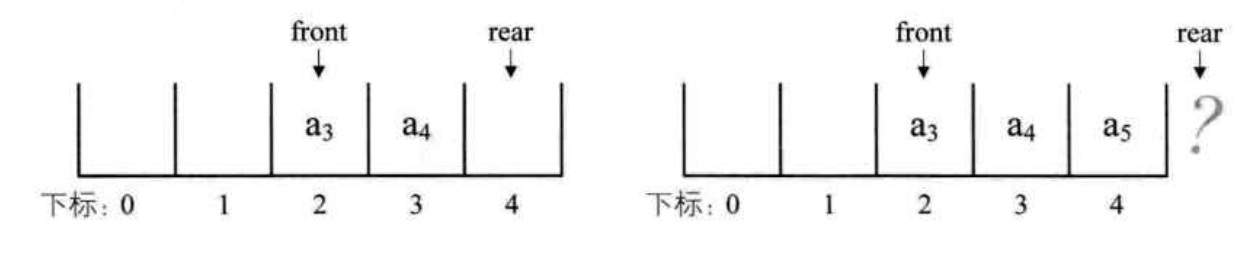
QueuePointeroverfolw

为了避免溢出，所以，我们在这种情况下，就让 rear 指针指向数组的 0 号元素，也就是头尾相接的循环。

图示如下

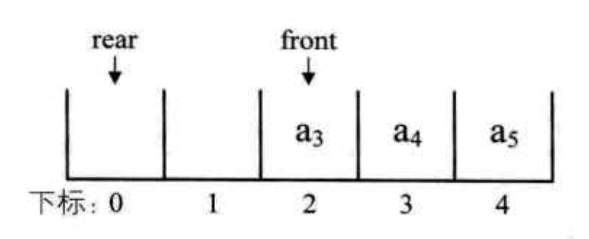
circularqueue

所以 循环队列，就是头尾相接的顺序存储结构

但是，当队列中的元素由于出列操作入列操作，被填满时， front 指针和 rear 指针又会重合，而我们在定义指针的时候，却定义了当两个指针重合的时候，是一个空队列，那么怎么解决这个问题呢？

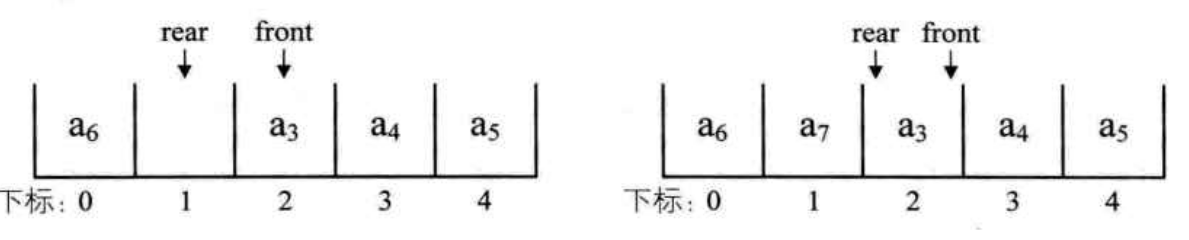
queueisfull

解决办法有两个：

  • 第一种是设置一个 flag 变量，flag 为 0 的时候，队列为空，flag 为 1 的情况，队列为满
  • 第二种，则是修改一下我们循环列表的定义
    • 当数组还剩余一个空闲空间时， 队列就满了，不能在进行入列操作了
    • 也就是如果数组的长度是 maxSize, 那么队列的最大长度就是 maxSize - 1
    • 当队列满了，rear 指针则指向数组的最后一个空闲空间

我们这里使用第二种方法： 下图就是队列满的情况

queueisfull2

如果设置数组长度为 QueueSize ：

  • 队列满的条件就是： (rear+1) % QueueSize == front
  • 队列的长度计算公式： （rear - front + QueueSize) % QueueSize

循环队列代码实现： https://github.com/ZhengshuaiPENG/DataStructure-Java/tree/master/src/org/lovian/datastructure/queue/sequencequque

循环队列的顺序存储结构代码：

java 实现如下：

public class SequenceQueue {
	private DataType[] data;
	private int front;	// 头指针
	private int rear;	// 尾指针

	public SequenceQueue(int maxSize) {
		// 初始化一个新的空队列
			this.data = new IntDataType[maxSize];
		this.front = 0;
		this.rear = 0;
	}
}

队列长度

public int length(){
	return (rear - front + data.length) % data.length;
}

入列操作

public boolean enQueue(DataType element) {
	// 如果队列满了
	if (((rear + 1) % data.length) == front)
		return false;
	// 插入新元素到队尾
	data[rear].SetData(element);
	// 后移rear指针
	// 若到了数组末尾则前移动到数组头部
	rear = (rear + 1) % data.length;
	return true;
}

时间复杂度 O(1)

出列操作

public boolean deQueue(DataType element) {
	// 如果队列为空
	if (rear == front)
		return false;
	// 拿到待删除元素
	element.SetData(data[front].getData());
	// 后移front指针
	// 若到了数组末尾则前移动到数组头部
	front = (front + 1) % data.length;
	return true;
}

时间复杂度 O(1)

4. 队列的链式存储结构

队列的链式存储结构，其实就是线性表的单链表，只不过只能尾进头出 而已，我们把它简称为链队列 ：

  • 队头指针 front： 链表头结点
  • 队尾指针 rear： 链表终端结点

为了操作的方便，我们将队头指针指向链队列的头结点，队尾指针指向终端节点

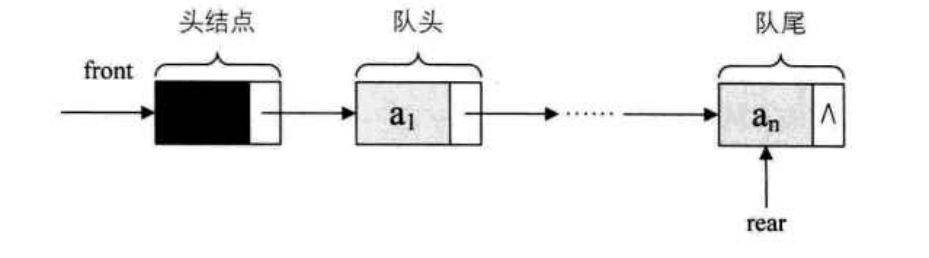
linkedqueue

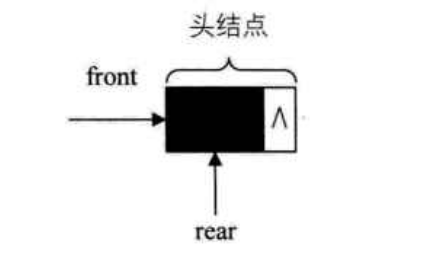
当链队列为空时，front 和 rear 都指向头结点

linkedqueue2

链队列代码实现： https://github.com/ZhengshuaiPENG/DataStructure-Java/tree/master/src/org/lovian/datastructure/queue/linkedqueue

链队列的存储结构代码

package org.lovian.datastructure.queue.linkedqueue;

import org.lovian.datastructure.data.DataType;

public class LinkedQueue {

private Node front; // 头指针，指向头结点
	private Node rear; // 尾指针，指向终端结点

	public LinkedQueue() {
		// 初始化空链队列，实际上只有一个队列对象
		this.front = new Node();
		// front = rear 时，队列为空
		this.rear = front;
	}
}

class Node {
	private DataType data;
	private Node next;

	public DataType getData() {
		return data;
	}

	public void setData(DataType data) {
		this.data = data;
	}

	public Node getNext() {
		return next;
	}

	public void setNext(Node next) {
		this.next = next;
	}
}

链队列的入列操作

public boolean enQueue(DataType element) {
	// 新建结点
	Node s = new Node();
	s.setData(element);
	// 将结点插入队尾
	rear.setNext(s);
	// 将尾指针后移
	rear = s;
	return true;
}

时间复杂度 O(1)

链队列的出对列操作

public boolean deQueue(DataType element) {
	// 如果队列为空，则 dequeue 失败
	if (front.equals(rear))
		return false;
	// 如果不为空，拿到第一个结点
	Node p = front.getNext();
	// 得到要删除的值
	element.SetData(p.getData().getData());

	// 如果删除的是最后一个结点，那么需要重置 front 和 rear 的值
	if (p.getNext() == null) {
		front = rear;
		return true;
	}
	front.setNext(p.getNext());
	return true;
}

时间复杂度 O(1)

Share this on