数值结构之图 Graph

I. 图

1. 图的定义

图 Graph ： 是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示成 G(V, E), 其中 G 表示一个图，V 是图中顶点的集合，E 是图 G 中边的集合

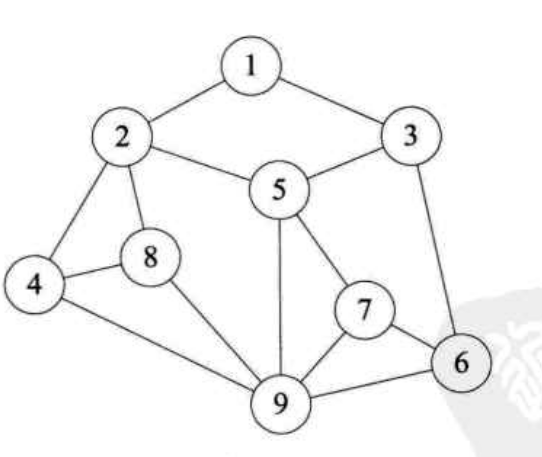
注意：

• 线性表中我们把数据元素叫做元素; 树中将数据元素叫做结点; 在图中数据元素我们称之为顶点 vertex
• 线性表可以有空表; 树可以有空树; 但是图中不允许没有顶点
• 线性表中，相邻的元素之间具有线性关系; 树中，相邻两层的结点具有层次关系; 在图中，任意两个顶点之间都可能有关系，顶点之间的逻辑关系用边来表示，边集可以是空的

2. 一些概念

• 无向边：
  • 若顶点 Vi 到 Vj 之间的边没有方向，则称这条边为无向边 （Edge）
  • 用无序偶对（Vi， Vj）来表示
  • 如果图中任意两个顶点之间的边都是无向边，那么称该图为无向图 Undirected graphs
• 无向完全图
  • 在无向图中，如果任意两个顶点之间都存在边，那么该图为无向完全图
  • 含有 n 个顶点的无线完全图有 n*(n-1)/2 条边
• 有向边：
  • 若从顶点 Vi 到 Vj 之间的边有方向，则称这条边为有向边，也叫弧（Arc）
  • 用有序偶对 <Vi, Vj> 来表示， Vi称为弧尾 tail， Vj 称为弧头 head
  • 如果图中任意两个顶点之间的边都是有向边，那么称该图为有向图 Directed graphs
• 有向完全图：
  • 如果任意两个顶点之间都存在方向互为相反的两条弧，称之为有向完全图
• 简单图：
  • 在图中，若不存在顶点到其自身的边，且同一条边不重复出现，称这样的图为简单图
• 权：
  • 有些图的边和弧具有与它相关的数字，这种与图的边和弧相关的数叫做权（weight）
  • 权可以表示从一个顶点到另一个顶点的距离或者耗费
• 网：
  • 带权的图称为网

3. 图的顶点与边的关系

• 无向图：
  • 度 Degree ： 顶点 V 的度是和 V 相关联的边的数目，记为 TD(V)
• 有向图：
  • 入度 InDegree ： 以顶点 V 为头的弧的数目，记为 ID(V)
  • 出度 OutDegree ： 以顶点 V 为尾的弧的数目，记为 OD(V)
  • 顶点 V 的度： TD(v) = ID(v) + OD(v)

4. 连通图

• 路径 path：从一个顶点到另外一个顶点的边的集合
• 连通图 Connected Graph：
  • 在无向图 G 中，如果从顶点 V 到顶点 V’ 有路经，则 V 和 V’ 是连通的
  • 如果图中任意两个顶点 Vi, Vj 都是连通的，则 G 是连通图
  • 对于有向图，则成为强连通图
• 连通分量：无向图中极大连通子图称为连通分量
  • 要是子图
  • 子图要连通
  • 连通子图含有极大顶点数
  • 具有极大顶点数的连通子图包含依附于这些顶点的所有边

II. 图的实现

1. 图的抽象数据类型

ADT Graph
Data
	顶点的有穷非空集合和边的集合
Operation
	CreateGraph(*G, V, VR)		// 构造图
	DestroyGraph(*G)			// 如果图存在则销毁
	LocateVex(G, u)				// 若 G 中存在顶点 u， 则返回图中的位置
	GetVex(G, v)				// 返回图中顶点 v 的值
	PutVex(G, v, value)			// 将图 G 中顶点 v 赋值 value
	FirstAdjVex(G, *v)			// 返回顶点 v 的一个邻接顶点，若顶点在 G 中无邻接顶点则返回空
	NextAdjVex(G, v, *w)		// 返回顶点 v 相对于顶点 w 的下一个邻接顶点，若 w 是 v 的最后一个邻接点则返回空
	DeleteVex(*G, v)			// 删除图G中顶点 v 及其相关的弧
	InsertArc(*G, v, w)			// 在图中增加弧 <v,w>
	DeleteArc(*G, v, w)			// 在图中删除弧 <v,w>
	DFSTraverse(G)				// 深度优先遍历
	HFSTraverse(G)				// 广度优先遍历

2. 图的邻接矩阵

因为图是由顶点和边或弧两部分组成，所以用两个结构来分别存储：

• 顶点：用一维数组
• 边或弧： 用一个二维数组存点和点之间的关系

图的邻接矩阵 Adjacency Matrix 存储方式是用两个数组来表示图，一个一维数组来存储图中的顶点信息，一个二维数组（称为邻接矩阵）来存储图中边或弧的信息

设图 G 中有 n 个顶点，则邻接矩阵是一个 n*n 的方阵，定义为 arc[i][j]， 下图是一个无向图的邻接矩阵

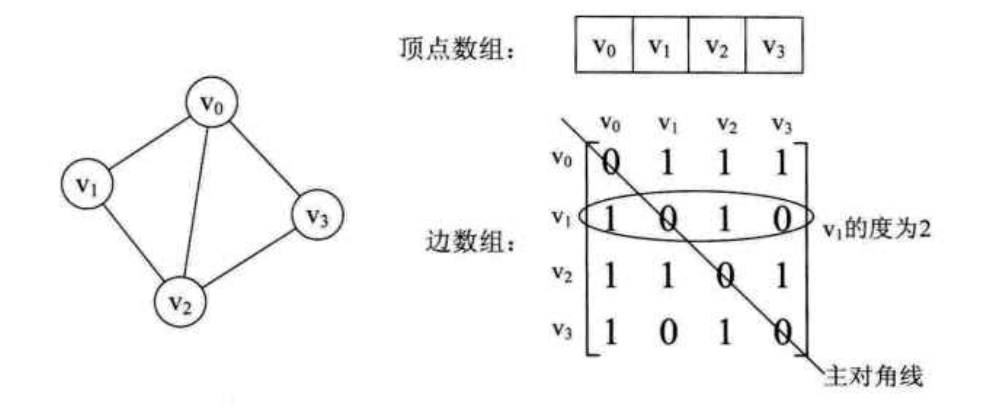
可以发现，无向图的边数组是一个对称矩阵

有了这个邻接矩阵，我们可以很容易的知道图中的信息：

• 判断任意两个顶点是否有边或者无边（看矩阵是否对称）
• 我们要知道某个顶点的度，其实就是这个顶点 Vi 在邻接矩阵中第 i 行（或者第 i 列）的元素之和，比如 v1 的度就是 1+0+1+0 = 2
• 求顶点 vi 的所有邻接点就是将矩阵中第 i 行元素扫描一遍，arc[i][j] 为 1 就是邻接点

再来看一个有向图的邻接矩阵：

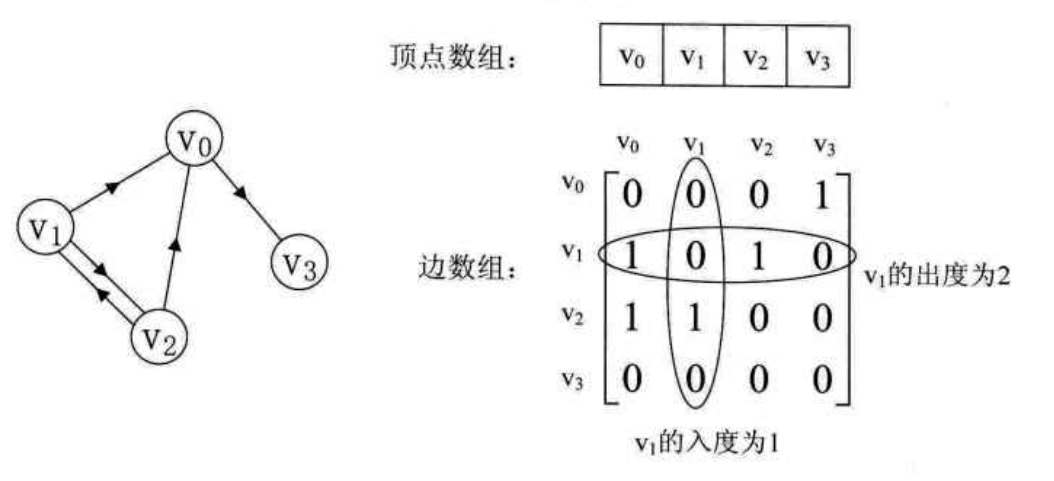
有向图的矩阵不对称，矩阵的行是出度，列是入度

3. 无向图存储结构的定义

package org.lovian.datastructure.graph;

import org.lovian.datastructure.data.DataType;
import org.lovian.datastructure.data.IntDataType;
import org.lovian.datastructure.data.IntWeightType;
import org.lovian.datastructure.data.WeightType;

public class UndirectedGraph {

	private static final int INFINITY = 65535; // 用 65535 来代表无穷

	private DataType[] vexs; // 存储顶点的一维数组
	private WeightType[][] arc; // 邻接矩阵
	private int numVertexes; // 图中当前顶点数
	private int numEdges; // 图中当前边数

	public UndirectedGraph(int maxVex) {
		// 最大的顶点数
		this.vexs = new IntDataType[maxVex];
		this.arc = new IntWeightType[maxVex][maxVex];
	}
}

4. 无向图其他操作

初始化无向图

public void initGraph(int numVertexes, int numEdges) {
	// 设置要生成图的顶点数和边数
	this.numVertexes = numVertexes;
	this.numEdges = numEdges;

	// 初始化邻接矩阵全部为无穷
	for (int i = 0; i < this.numVertexes; ++i) {
		for (int j = 0; j < this.numVertexes; ++j) {
			WeightType weight = new IntWeightType();
			weight.SetWeight(INFINITY);
			arc[i][j] = weight;
		}
	}

	// 读入 numEdges 条边，建立邻接矩阵
	Scanner sc = new Scanner(System.in);
	for (int k = 0; k < this.numEdges; ++k) {
		System.out.println("输入边 (Vi, Vj) 的下标 i：");
		int i = sc.nextInt();
		System.out.println("输入边 (Vi, Vj) 的下标 j：");
		int j = sc.nextInt();
		System.out.println("输入边 (Vi, Vj) 的权 w：");
		int w = sc.nextInt();
		arc[i][j].SetWeight(w);
	}
	sc.close();
}

时间复杂度 O(n^2)

5. 邻接表

邻接矩阵是一种比较不错的存储结构，但是，对于边数相对顶点较少的图，这种结构是存在对存储控件的极大浪费。所以我们考虑另外一种存储结构，用数组和链表相结合的存储方法称为邻接表 Adjacency Lsit:

• 图中的顶点用一个一维数组存储，当然，顶点也可以用单链表存储，但是数组更方便
• 图中每个顶点 vi 的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点 vi 的边表，有向图则称为 vi 作为弧尾的出边表

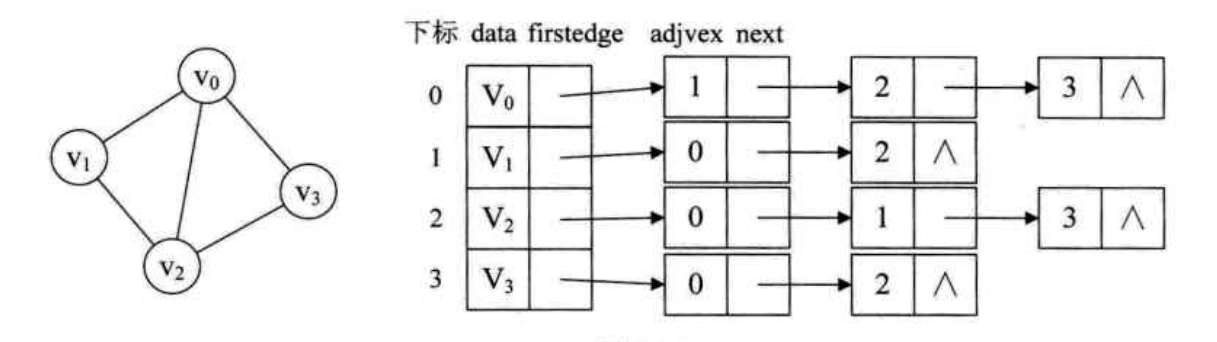
从图中我们可以看出：

• 顶点表的各个节点由 data 和 firstedge 两个域表示
  • data 是数据域，存储顶点信息
  • firstedge 是指针域，指向边表的第一个结点，即此顶点的第一个邻接点
• 边表结点由 adjvex 和 next 两个域组成
  • adjvex 是邻接点域，存储某顶点的邻接点在顶点表中的下标
  • next 存储指向边表中下一个结点的指针
  • 比如 v1 顶点与 v0、 v2互为邻接点，则在 v1 的边表中，adjvex 分别为 v0 的 0 和 v2 的 2

这样的结构我们要获得图中相关信息也很容易：

• 获取某个顶点的度： 查找这个顶点边表中结点的个数
• 判断两个顶点之间是否存在边： 测试顶点 vi 的边表中 adjvex 是否存在结点 vj 的下标 j
• 求顶点的所有邻接点，那么就是对此顶点的边表进行遍历，得到 adjvex 域对应的邻接点

对于待权值的网图，可以在边表结点定义中增加一个 weigth 数据域，存储权信息; 另外由于有向图有方向，用顶点为弧尾来存储边表的额，这样很容易得到每个顶点的出度，图示如下：

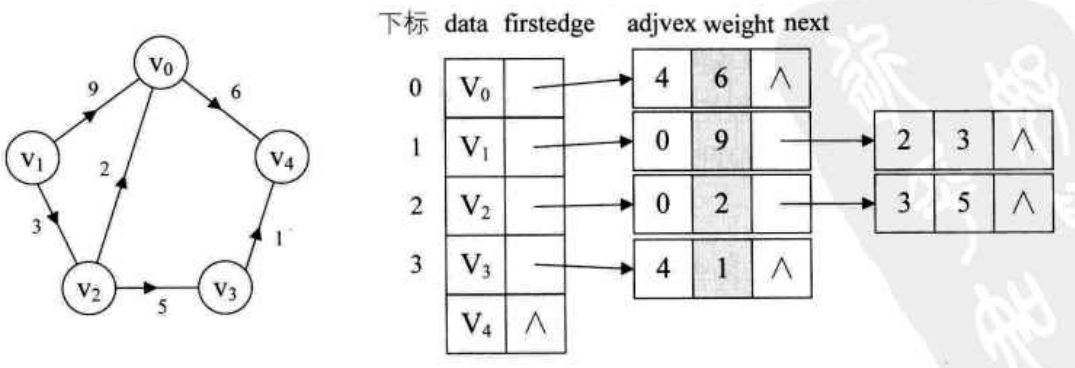
如果用顶点的弧头来建立边表，那么这就是一个逆向邻接表

6. 十字链表

由于邻接表在处理有向图时，只能得到某个顶点的出度，要得到入度的话，需要对整个图进行遍历，所以要同时方便的得到出度和入度信息，就要结合邻接表和逆向邻接表，这就是十字链表 Orthogonal List。

• 顶点表结点结构：
  • data ： 存储顶点数据
  • firstin ：入边表头指针，指向该顶点的入边表中的第一个结点
  • firstout ：出边表头指针，指向该顶点出边表中的第一个结点
• 边表结点结构 ：
  • tailvex : 弧起点在顶点表的下标
  • headvex : 弧终点在顶点表的下标
  • headlink :入边表指针域，指向终点相同的下一条边
  • taillink :出边表指针域，指向起点相同的下一条边
  • weigth ： 权值

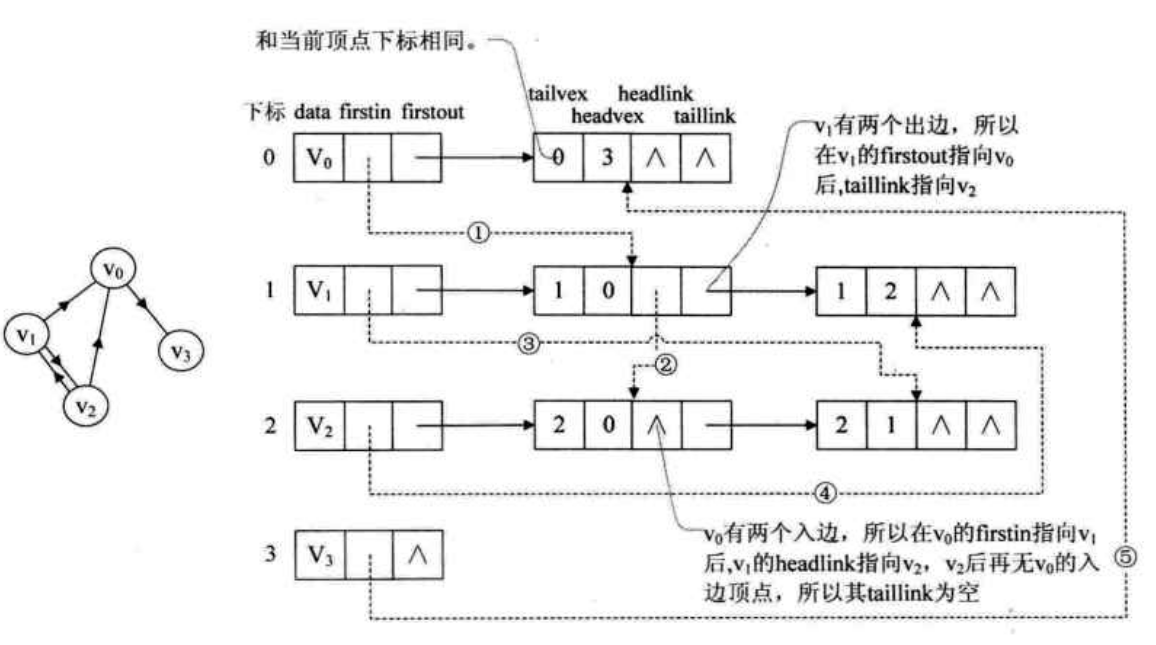
在图中，虚线箭头其实就是此图的逆邻接表的表示，对于 v0 来说， 它有两个顶点 v1 和 v2 的入边， 因此 v0 的firstin 指向顶点 v1 的边表结点中 headvex 为 0 的结点，接着由入边结点的 headlink 指向下一个入边顶点 v2。对于顶点 v1, 它有一个入边顶点 v2, 所以它的 firstin 指向顶点 v2 的边表结点中 headvex 为 1 的结点。顶点 v2 和 v3 也是同样有一个入边顶点

III. 图的遍历

图的遍历和树的遍历类似，从图中某一个顶点出发遍历图中其余顶点，且使每一个顶点仅被访问一次。

在树的遍历中有四种方法，但是树的根结点只有一个，遍历都是从根结点开始。但是在图中，因为它的任何一个顶点都可能和其余的所有顶点相邻接，极有可能沿着某条路经搜索之后，又回到了原顶点，而有些顶点却还没有遍历到。所以我们要在遍历的过程中，把访问过的顶点打上标记。具体办法是，设置一个访问数组 visted[n], n 是图中顶点的个数，初值为 0,访问过后设置为 1。遍历的方式有两种：深度优先遍历和广度优先遍历。

1. 深度优先遍历

深度优先遍历 Depth First Search, 也叫深度优先搜索 （DFS）。

深度优先遍历实际上就是一个递归的过程，有点类似树的前序遍历： 从图中某个顶点 v 出发， 访问此顶点，然后从 v 的未被访问的邻接点出发深度优先遍历图，直到图中所有和 v 有路径相通的顶点都被访问到

我们用代码来实现下图的遍历：

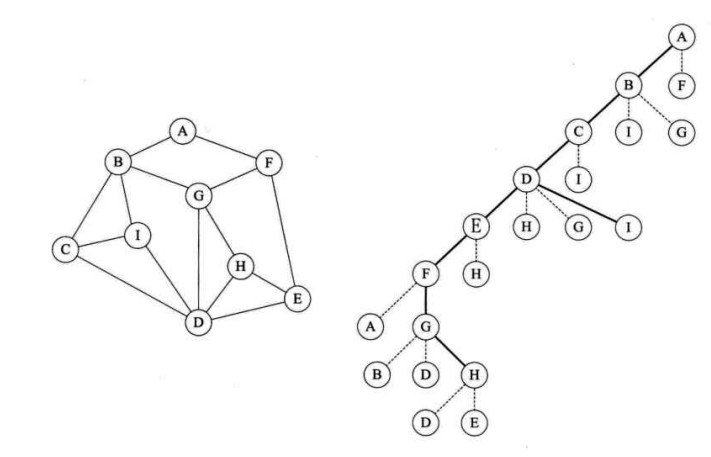
C++代码实现：（邻接矩阵）

typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */

#define MAXSIZE 9 /* 存储空间初始分配量 */
#define MAXEDGE 15
#define MAXVEX 9

typedef struct
{
    VertexType vexs[MAXVEX]; /* 顶点表 */
    EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */
    int numVertexes, numEdges; /* 图中当前的顶点数和边数 */
} MGraph;

bool visited[MAXVEX];/* 访问标志的数组 */
/* 邻接矩阵的深度优先递归算法 */
void DFS(MGraph MG, int i)
{
    int j;
    visited[i] = true;
    cout << MG.vexs[i] << ' '; /* 打印顶点，也可以其它操作 */
    for (j = 0; j < MG.numVertexes; j++)
        if (MG.arc[i][j] == 1 && !visited[j])
            DFS(MG, j);/* 对为访问的邻接顶点递归调用 */
}
/* 邻接矩阵的深度遍历操作 */
void DFSTraverse(MGraph MG)
{
    int i;
    for (i = 0; i < MG.numVertexes; i++)
        visited[i] = false;/* 初始所有顶点状态都是未访问过状态 */
    for (i = 0; i < MG.numVertexes; i++)
        if (!visited[i])
            DFS(MG, i);/* 对未访问过的顶点调用DFS，若是连通图,只会执行一次*/
}

遍历顺序： A B C D E F G H I

2. 广度优先遍历

广度优先遍历 Breadth First Search， 也叫广度优先搜索 （BFS）

广度优先遍历类似于树的层序遍历，如下图：

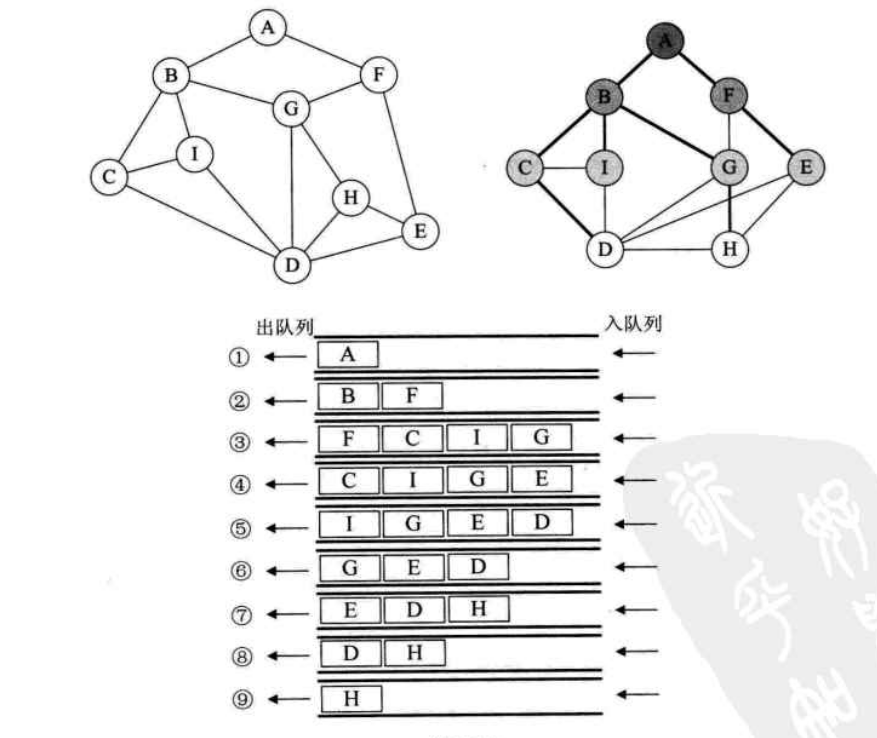
我们把图的顶点，根据其邻接点来进行分层变形，但实际上顶点和边的关系没有发生变化。然后对每一层的顶点进行遍历，

C++代码如下：(邻接矩阵)

typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */

#define MAXSIZE 9 /* 存储空间初始分配量 */
#define MAXEDGE 15
#define MAXVEX 9

typedef struct
{
    VertexType vexs[MAXVEX]; /* 顶点表 */
    EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵，可看作边表 */
    int numVertexes, numEdges; /* 图中当前的顶点数和边数 */
} MGraph;

/* 邻接矩阵的广度遍历算法 */
void BFSTraverse(MGraph G)
{
    int i, j;
    Queue Q;
    for (i = 0; i < G.numVertexes; i++)
        visited[i] = false;
    InitQueue(&Q);/* 初始化一辅助用的队列 */

    for (i = 0; i < G.numVertexes; i++)/* 对每一个顶点做循环 */
    {
        if (!visited[i])/* 若是未访问过就处理 */
        {
            visited[i] = true;/* 设置当前顶点访问过 */
            cout << G.vexs[i] << ' '; /* 打印顶点，也可以其它操作 */
            EnQueue(&Q, i);/* 将此顶点入队列 */
            while (!QueueEmpty(Q))/* 若当前队列不为空 */
            {
                DeQueue(&Q, &i);/* 将队对元素出队列，赋值给i */
                for (j = 0 ; j < G.numVertexes; j++)
                {
                    /* 判断其它顶点若与当前顶点存在边且未访问过  */
                    if (G.arc[i][j] == 1 && !visited[j])
                    {
                        visited[j] = true;/* 将找到的此顶点标记为已访问 */
                        cout << G.vexs[j] << ' '; /* 打印顶点 */
                        EnQueue(&Q, j);/* 将找到的此顶点入队列  */
                    }
                }
            }
        }
    }
}

遍历结果为：A B F C G I E D H

3. 深度优先和广度优先的另一种理解

广度优先遍历 BFS：

• 浅尝辄止，每个顶点只访问邻接结点（如果邻接结点没有被访问过），并且记录这个邻接结点，当访问完它的邻接结点之后就结束这个顶点的访问。
• BFS 用到了 FIFO 队列，通过这个队列来存储第一次发现的结点，对于再次发现的结点，不放入队列

Function BFS(G = (V,E): graph; s: vertex of G) : List of vertices
// G is a connected graph of order n
// Vertices of G are labeled from 1 to n
// s is a vertex of G
// Return a list (a queue) of all vertices, ordered by the order of visit
VARIABLES
	Visited : Queue
	// Visited is the list of visited vertices
	Q : Queue
BEGIN
	Visited ← enqueue(s,emptyQueue)
	Q ← enqueue(s,emptyQueue)
	WHILE Q is not empty DO
		i ← dequeue(Q)
		FOR ALL edge {i,j} in E DO
			IF j is not in Visited THEN
				enqueue(j,Visited)
				enqueue(j,Q)
			END IF
		END FOR
	END WHILE
	RETURN Visited
END

深度优先遍历 DFS：

• 打破砂锅问到底，访问一个顶点后，继而访问下一个邻接的顶点，如此往复直到当前顶点被访问或者它不存在邻接的顶点
• DFS 可以理解为用到了 Stack 的策略（递归调用）

IV. 最小生成树

一个连通图的生成树，是一个极小的连通子图，它含有图中所有的顶点，但只有足以构成一棵树的 n-1 条边，我们把构造连通网的最小代价生成树称为最小生成树 Minumum Cost Spanning Tree。其实，就是带权图对应的生成树, 生成树各边的权值总和称为生成树的权。权最小的生树称为最小生成树。比如规划最小成本架设电线塔。

找连通网的最小生成树有两种算法： Prim 算法和 Kruskal 算法

1. Prim 算法

Prim 算法从点入手，不断扩大点集合，并在以点集合中所有点相关的边中权值最小的且不构成回路的，不断加入集合，最终构成最小生成树。

对于图G=（V，E），Prim算法描述如下：

1、给定空集合A，以及任何一点v0属于{V}，将v0加入集合A中，此时A={v0}。

2、对于集合A中的任意一点u，以及V-A中任意一点w，找到权重最小的边（u，w）

3、判断步骤2中的边（u，w）是否使图A形成回路，如果形成回路，则不加入A，否则将点w和边（u，w）加入A。

4、判断此时图G中所有点{V}是否已经全部加入到集合A中，如果是，则最小生成树已经找到，返回 A；否则，继续步骤2。

伪代码如下

Function Prim(G=(V,E,W):graph): graph
	% Precondition: G connected
BEGIN
	Chose (randomly) a vertex v from V(G)
	T ← ({v},{})
	WHILE V(T) ⊊ V(G) DO
		Chose e = {v,v’} such that
		v ∈ V(T) and v’ ∉ V(T) and W(e) minimal
		T ← T + e
	END WHILE
Return T
END

2. Kurskal 算法

Prim 算法是以某个顶点为起点，逐步找各个顶点上最小权值的边来构建最小生成树的。同样的思路，我们可以直接以边为目标去构建，因为权值是在边上，所以直接去找最小权值的边来构成生成树。

对于图G=（V，E），Kruskal算法描述如下：

2、将图G中所有边按照权重进行排序，形成有序集合B。

3、对于步骤2中排序后集合B中权重最小的边（u，v），尝试将（u，v）以及点u、v加入到集合A中。

4、如果步骤3中尝试加入的点和边，对于图A而言，不形成回路，则添加点u、v及边（u，v），否则不添加。

5、将步骤3处理的边（u，v）从集合B中删除。

伪代码如下：

FUNCTION Kruskal(G=(V,E): graph): graph
	G weighted connected graph
	result: A MST
BEGIN
	F = E
	T = a set of edges
	Initialize T to empty
	WHILE |T|<n-1 DO
		Find an minimum weighted edge e of F
		F := F - e
		IF T + e is acyclic THEN
			T := T + e
		END IF
	END WHILE
	Return (V,T)
END

V.最短路径

最短路径： 是指两顶点之间经过的边上权值之和最少的路径，路径上的第一个顶点是源点，最后一个顶点是终点。

最短路径典型应用场景就是规划地铁路线

1. Dijkstra 算法

Dijkstra 算法是单源图最短路算法：

• 输入
  • 连通有权图
  • 起点 s
  • 所有边权非负
• 输出
  • 起点到各个结点的最短路长度

思路：

1、初始时，S只包含源点，即S＝{v}，v的距离dist[v]为0。U包含除v外的其他顶点，U中顶点u距离dis[u]为边上的权值（若v与u有边） ）或∞（若u不是v的出边邻接点即没有边<v,u>）

2、从U中选取一个距离v(dist[k])最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）

3、以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u（u∈ U）的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。即如果dist[k]+w[k,u]<dist[u]，那么把dist[u]更新成更短的距离dist[k]+w[k,u]

4、重复步骤（2）和（3）直到所有顶点都包含在S中(要循环n-1次)

伪代码如下：

Function Dijkstra(G = (V,E,W): graph; s: vertex of G): Tree
// G is of order n, connected and with positive weights
// Return a tree of shortest path from s to all other vertices
VARIABLES
	d: table [1..n]
	// d(i) is the distance from s to i
	father : table [1..n]
	// father(i) is the predecessor of i in a shortest path from s to i
	1M: set of vertices with a known shortest distance from s
	E’: set of edges of the return tree
BEGIN
	FOR i FROM 1 TO n DO
		d(i) := +∞
	END FOR
	d(s) := 0
	M := {}
	WHILE M 6 = V DO
		Chose i in V - M with minimum d(i)
		M := M + i
		FOR ALL j successor of i DO
			IF d(i) + W(i,j) < d(j) THEN
				d(j) := d(i) + W(i,j)
				father(j) := i
			END IF
		END FOR
	END WHILE
	// Construction of the tree
	E’ :=
	FOR i FROM 1 TO n, i 6 = s DO
		E’ := E’ + (father(i),i)
	END FOR
	Return (V,E’)
END