数值结构之栈 Stack

I. 栈

1. 栈与队列

• 栈 Stack ： 是限定仅在表尾为进行插入和删除操作的线性表
• 队列 Queue ：是只允许在一段进行插入操作，而在另一端进行删除操作的线性表

2. 什么是栈

栈 Stack：

• 仅在表尾进行插入和删除操作的线性表
• 栈是后进先出的线性表
  • LIFO： Last In First Out
• 允许插入和删除的一端叫做栈顶 top， 另一端叫栈底 bottom

3. 栈的性质

理解栈的定义，要注意如下几点：

• 栈首先是个线性表，栈元素具有线性关系，即前驱后继关系
• 在线性表的表尾进行插入和删除操作，这里的表尾是指 栈顶
• 栈底是固定的，先进栈的只能在栈底
• 栈的插入操作，叫做进栈，也叫压栈，入栈
• 栈的插入操作，叫做出栈，也叫做弹栈
• 可以把栈理解成子弹夹

栈的进栈出栈示意图：

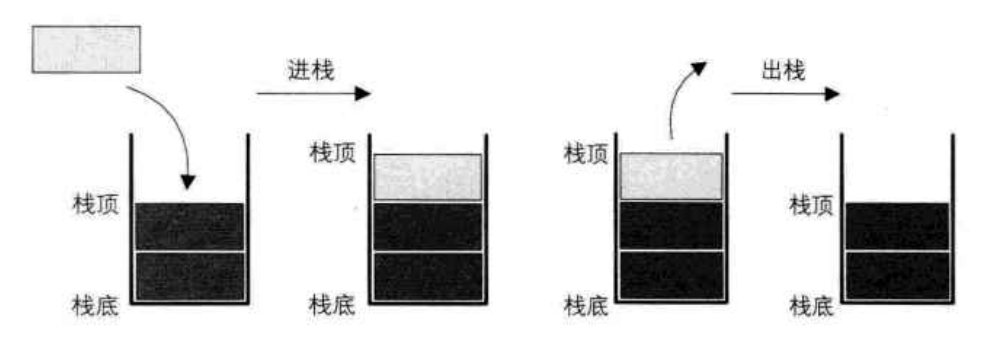
4. 进栈处栈变化形式

举例来说，如果现在有 3 个整型数字元素 1， 2, 3 依次进栈，会有如下出栈次序：

• 第一种： 1, 2, 3 进， 再 3, 2, 1 出，出栈次序是 3, 2, 1
• 第二种： 1 进 1 出， 2 进， 2 出， 3 进 3 出， 也就是进一个就出一个，出栈次序为 1， 2， 3
• 第三种： 1 进 2 进， 2 出 1 出， 3 进 3 出， 出栈次序为 2, 1, 3
• 第四种： 1 进 1 出， 2 进， 3 进， 3 出， 2 出， 出栈次序为 1， 3, 2
• 第五种： 1 进 2 进， 2 出， 3 进， 3 出， 1 出， 出栈次序为 2, 3, 1

如果元素数量多，出栈的变化将会更多

II 栈的实现

1. 栈的抽象数据类型

对于栈来说，理论上线性表具备的操作特性它都具备，由于操作上的特殊性，所以针对它的操作上有变化，特别是插入和删除操作：

• 插入： 进栈，压栈 push
• 删除： 出栈，弹栈 pop

ADT Stack
Data
	DataType {a0, a2, ..., an−1}
Operation
	InitStack(*S) // 初始化操作，建立一个空栈 S
	DestroyStack(*S) // 若栈存在，则销毁它
	ClearStack(*S) // 将栈清空
	StackEmpty(S) // 若栈为空，返回 true， 否则返回 false
	GetTop(S, *e) // 若栈存在且非空，用 e 返回 S 的栈顶元素
	Push(*S, e) // 若栈 S 存在，插入新元素 e 到栈 S 中并称为栈顶元素
	Pop(*S, *e) // 删除栈 S 中栈顶元素， 并用 e 返回其值
	StackLength(S) // 返回栈 S 的元素个数
endADT

2. 栈的顺序存储结构

栈的顺序存储结构代码： https://github.com/ZhengshuaiPENG/DataStructure-Java/tree/master/src/org/lovian/datastructure/stack/sequencestack

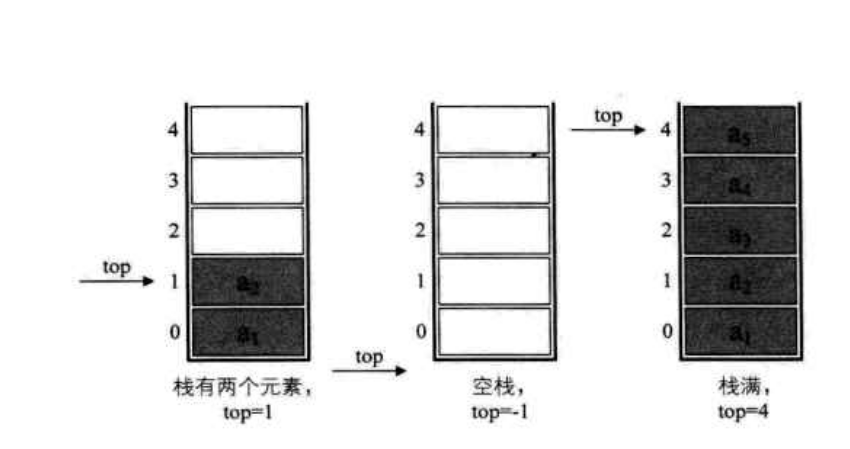
在栈的顺序结构中我们用数组来当作栈的底层， 下标为 0 的一端作为栈底。

定义一个 top 指针变量来指示栈顶元素在数组中的位置，top 指针必须小于栈的长度 stackSize, 当栈存在一个元素，top 等于 0，因此通常把空栈的判定条件定位 top 等于 -1

public class Stack {
	private DataType[] data;
	private int top; // 栈顶指针

	public Stack(int stackSize) {
		// 设置栈的长度为 stackSize
		data = new IntDataType[stackSize];
	}
}

如果现在有一个栈， stackSize 是 5, 则栈的普通情况， 空栈，和栈满的情况示意图如下图所示

插入操作

对于栈的插入，就是进栈操作 push：

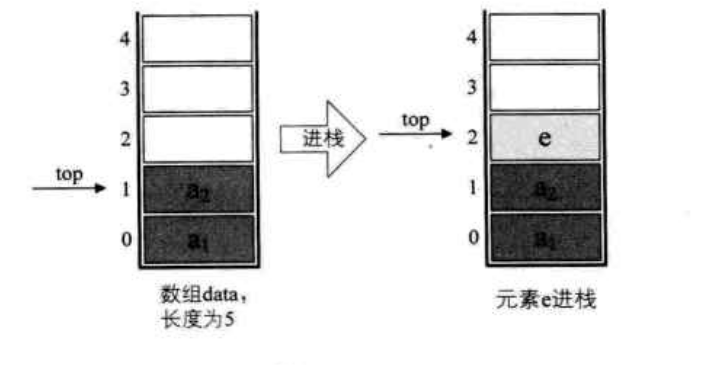
Java 实现如下：

public boolean push(DataType element){
	// 如果栈满了
	if(top == data.length - 1)
		return false;

	top++;
	data[top] = element;
	return true;
}

删除操作

对于栈的删除，就是弹栈操作 pop：

Java 实现如下：

public boolean pop(DataType element){
	// 如果栈为空
	if(top == -1)
		return false;
	element.SetData(data[top].getData());
	top--;
	return true;
}

push 和 pop 操作的复杂度都是 O(1)

3. 栈的链式存储结构

栈的链式存储结构代码： https://github.com/ZhengshuaiPENG/DataStructure-Java/tree/master/src/org/lovian/datastructure/stack/linkedstack

由于顺序的栈结构的大小是固定的，所以有时侯不知道数组的长度，就有了栈的链式存储结构，简称为链栈：

• 栈顶放在链表的头部
• 不存在头结点和头指针
• 有栈顶指针 top
• 链栈为空的时候，就是 top = null

java 实现如下：

public class LinkedStack {
	private Node top;
	private int count;

	public LinkedStack() {
		// 空的栈链，top = null
		this.count = 0;
	}


}


class Node{
	private DataType data;
	private Node next;

	public DataType getData() {
		return data;
	}
	public void setData(DataType data) {
		this.data = data;
	}
	public Node getNext() {
		return next;
	}
	public void setNext(Node next) {
		this.next = next;
	}
}

插入操作

链栈的插入，就是把待插入结点 s 插入到栈的顶部，也就是链表的头部：

public boolean push(DataType element){
	// 待插入结点
	Node s = new Node();
	s.setData(element);

	// 将待插入的结点的后继设置成当前的top
	s.setNext(top);
	// 让新插入栈顶的结点成为新的 top
	top = s;
	count++;
	return true;
}

时间复杂度 O(1)

删除操作

链栈的删除，就是将当前栈顶的 top 结点的后继结点，设置成新的 top 结点

public boolean pop(DataType element){
	// 如果链栈为空
	if(top == null)
		return false;
	// 拿到当前的栈顶 top 结点中保存的数据
	element.SetData(top.getData().getData());
	// 设置原来 top 结点的后继为新的 top
	top = top.getNext();
	count--;
	return true;
}

时间复杂度为 O(1)

4. 顺序栈和链栈的选择

如果栈的使用过程中，元素的变化不可预料，有时很小，有时非常大，那么最好使用链栈，反之，如果元素的变化在可控的范围内，那么使用顺序栈会更好一点

III. 栈的应用

1. 递归

递归： recursive

• 把一个直接调用自己或通过一系列的调用语句间接的调用自己的函数，称作递归函数
• 必须存在递归基： 当递归调用调用到递归基时，就退出递归

2. 栈与递归的关系

递归过程的退回，就是递归过程的前行顺序的逆序，在退回过程中，可能要执行某些动作，包括恢复在前行过程中存储的某些数据。 这种存储某些数据，并在后面又以存储的逆序来恢复这些数据，以提供使用的需求，就非常符合栈这样的数据结构，所以编译器使用栈来实现递归